Mutual Funds Day 39: Standard Deviation
In the last few chapters, we discussed diversification & how it is getting measured. If you have not read those chapters, please do so.
https://viswaram.com/mutual-funds-day-36-the-concept-of-diversification-862bf544e2achttps://viswaram.com/mutual-funds-day-36-the-concept-of-diversification-862bf544e2achttps://viswaram.com/mutual-funds-day-36-the-concept-of-diversification-862bf544e2ac
In the current chapter, we will discuss the standard deviation. The definition is the amount of dispersion of the measured instrument from its mean, but to explain it in detail we might have to learn about:
- Mean
- Variance
Mean: If you sum up all the values of an outcome and then divide it by the number of instances in which we got the outcome, we get the average value or the mean.
For example, if the runs scored by Ramesh in the last 5 cricket matches are 61, 22, 102, 76, 12 then the sum = 273 and mean = 273/5 = 54.6. The next time when he goes out to bat, the spectators expect him to score runs quite close to his average of 54.6. Mean is the easiest to measure, but it does not give the exact picture of an outcome.

Variance: This is the measure of the dispersion of a value from its mean. The mathematical formula to calculate variance is to deduct the mean from each outcome and square it. Once its squared, it is added with the other outcomes, and the total value is divided by the number of outcomes.
In our case, variance = [(54.6–61)²+(54.6–22)²+(54.6–102)²+(54.6–76)²+(54.6–12)² ]/5 = 5623.2/5 = 1124.64.
Once we calculate the variance, it is pretty straightforward to calculate the standard deviation as it is the square root of variance.
Standard deviation = sqrt of 1124.64 = 33.54
If we go back to the original example, we can say with high confidence that Ramesh will score between 54.6–33.54 and 54.6+33.54, ie between 21.06 & 88.14.
Our confidence level will be much higher if we take 2 standard deviations ie 33.54×2 = 67.08 and the highest if we take 3 SD ie 33.54×3 = 100.62
Now if you were the coach of Ramesh and you had to choose between Ramesh (SD = 33.54) and Suresh (SD = 8) for the next match, you may end up selecting Suresh as his standard deviation is lesser.
A lower standard deviation means a lower risk and a higher standard deviation means a higher risk.
But when it comes to selecting a mutual fund people end up selecting the ones with higher SD with the impression that a higher risk will give higher returns. My personal opinion is that, SD is just 1 factor of the many that you need to consider before finalizing what mutual funds to buy.
Examples
- SBI Contra fund has an SD of 13.08
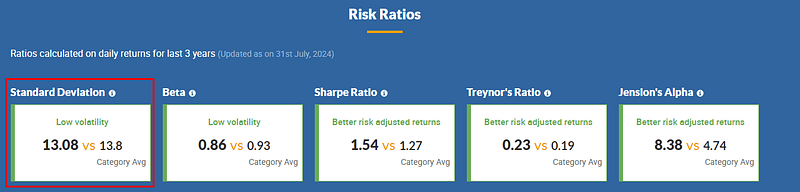
2. BOI Flexi cap fund has an SD of 16.45

3. ITI Small Cap fund has an SD of 17.26

The respective benchmark standard deviations are also mentioned as the 3 funds I have selected are not from the same category.
Next Chapter
https://viswaram.com/mutual-funds-day-36-the-concept-of-diversification-862bf544e2ac
If you liked this content, consider sharing it with your friends & relatives..
Book a free consultation — Get your mutual fund holdings audited based on your risk profile — https://learn.viswaram.com/knowmore
https://viswaram.com/mutual-funds-day-36-the-concept-of-diversification-862bf544e2ac
